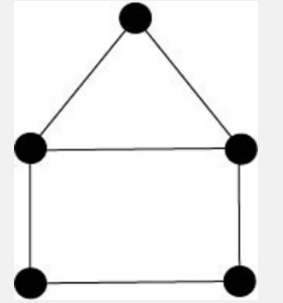
你有没有尝试过做下面的脑筋急转弯，你必须把这些点连接起来，连续一笔画出一座房子的轮廓，而不需要回头看你的线条?或者您可能点击过 Facebook 的好友推荐或玩过《卡坦岛》。

如果是这样，您已经体验过某种形式的图论，这是一个让中国西交利物浦大学 的 刘旭军博士着迷的数学领域 。

“我最初的计划是追求不同的数学领域，但我被图论中证明思想的优雅和美丽所吸引，”刘博士说。

从A到B

图论是数学的一个分支，它探索图的关系和属性——但我们讨论的不是饼图和散点图。

那么什么是图表呢?

假设您想找出乘坐火车往返于伦敦和维也纳之间最有效的方式。您可以将每个城市绘制为一个点(在数学中称为顶点)，并将城市之间的路线绘制为直线或曲线(称为边)。这种顶点和边的组合构成了一个图。

然后该图可用于研究两个城市之间的连接和路线。

图论可以帮助数学家建模和分析各个领域的复杂网络，包括计算机科学和电气工程。

刘博士与 大谷州立大学的Michael Santana博士和Taylor Short博士合作，最近解决了一个 引起图论研究人员广泛关注的问题。

给我涂上不同的颜色

该团队的研究涉及图论的一个方面，称为着色。着色理论处理标记图形各部分以遵守某些规则并避免特定冲突的问题。

例如，假设您想要为下面的每个点着色，这样就不会有两个相邻的相同颜色的点 - 这是着色的示例。

刘博士解释说：“我研究一种称为打包着色的着色，它是通过广播网络中的频率分配问题实现的。

“世界上有很多广播电台，我们希望为每个电台分配一个频率;分配相同频率的电台要求至少相距一定的距离，并且每个频率需要不同的最小距离。

“这个问题引起的问题之一是‘这样的分配所需的最少频率数量是多少?’”

战略发展

在他最近的工作中，刘博士和他的合作者成功解决了数学家 Hocquard、Lajou 和 Lužar 在 2022 年《图论杂志》上提出的问题。

该问题涉及次立方图的划分，其中每个顶点(点)最多有三个边(线)附加到它。

考虑到有两种不同类型的边，任务是确定如何将边划分为多个类：

类型 I - 要求每对边不共享端点(每条边有两个端点)。

类型 II - 要求其中的每对边不仅不共享端点，而且它们的端点不由另一条边连接。

该团队着手解决的问题是，是否可以在将 I 类类别的数量固定为 1 的同时，最大限度地减少 II 类类别的数量。

刘博士说：“通过解决这个猜想，我们为增强我们对次立方图的结构特性的理解做出了重大贡献，并可能为解决著名的 Erdős-Nešetřil 猜想提供见解。

“它还可以为解决通信网络中的问题提供指导。”